Электрон — кольцо Максвелла-Герца

See english version of this article

Предложена модель электрона в виде кольца максвелловского тока смещения.  Определены параметры такой модели свободного электрона.  Показано, что известная постоянная тонкой структуры  может трактоваться  как параметр этой модели.

Со времени открытия электрона  Джозефом Томсоном в 1897 году до сих пор обсуждается вопрос о его структуре и размерах [1].  Существуют взгляды экспериментаторов, основанных на сечениях рассеяния, что электрон – это шар диаметром 10^-17~10^-18 м.  Известна теоретическая константа – так называемый  классический радиус электрона

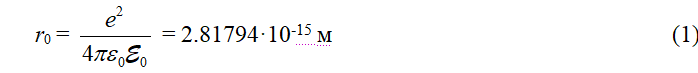
В современной квантовой физике вопрос о структуре электрона не рассматривается.

В XIX веке Джеймс Максвелл, чтобы получить решение в виде электромагнитной волны, ввел в свои уравнения так называемый ток смещения.  В данной работе предлагается модель электрона  в виде тора – заряженного кольца максвелловского тока смещения.

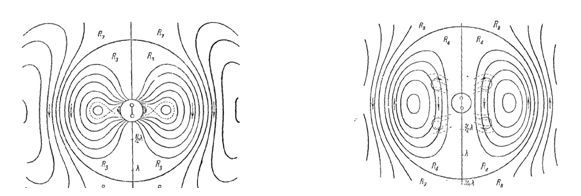
После известного эксперимента по рассеиванию рентгеновского излучения на свободных электронах (1923), Артур Комптон пытался предложить научному сообществу модель электрона-кольца.  Еще ранее, аналогичные кольца, но радиофотонов, нарисовал своей рукой Генрих Герц после своих знаменитых опытов с излучением электрического диполя.

Пусть  r_e – радиус кольца тора,  b – радиус сечения тора  (1/2 толщины)

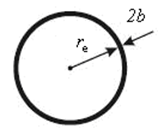
Рис.1.  Кольцо тока смещения

Введем обозначение форм-фактора кольца 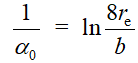. Будем считать, что заряд и ток сосредоточены в поверхностном слое тора.  Тогда формулы для электрической емкости и индуктивности кольца  [2] записываются в виде

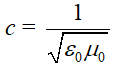Разобьем собственную энергию электрона  (энергию покоя)  = m_ec² = 8.18724*10^-14 дж  на две одинаковые части: = m_ec²/2 + m_ec²/2,  где – скорость света.

Одна часть – это энергия электрического (кулоновского) поля вокруг одиночного заряда  (e):

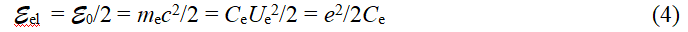
где потенциал  U_e,  емкость  C_e  и  квант заряда электрона  (e)  связаны соотношением

e = C_e·U_e                                                                                (5)

Вторая часть энергии электрона – это энергия магнитного поля (МП)  кольца тока

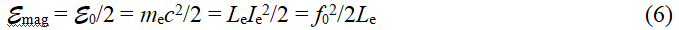
где  f₀ – магнитный поток кольца электрона.  Считаем, что он равен известному кванту магнитного потока

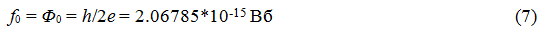
f₀  связан с током  I_e  и индуктивностью кольца  L_e  соотношением

Равенство энергий  и приводит к уравнению  e²/2C_e  = f₀²/2L_e. Учитывая (2) и (3)  получаем формулу для форм-фактора кольца

Учитывая (3) и (6)  получаем формулу для энергии МП кольца

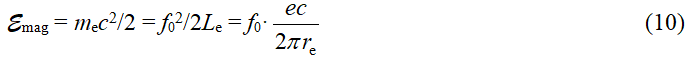
Здесь очевидна простая интерпретация: 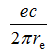   – это ток смещения, эквивалентный вращению заряда (e)  вдоль окружности радиуса  r_e  со скоростью света  (c),  а  f₀ – мультипликативный коэффициент.  Чем меньше размер частицы, тем короче путь тока,  больше сам ток  и  энергия частицы. Энергию МП можно также трактовать как энергию вращения распределенной инертной массы  m_e  по окружности кольца со скоростью света.  Видим, что это совпадает с классической зависимостью кинетической энергии  от скорости движения  ,  где

Из формулы полной энергии электрона с учетом (7)   = m_ec² = 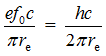мы видим, что она эквивалентна определению комптоновской длины волны электрона, введенной после экспериментов Артура Комптона  в 1923г

Безразмерная постоянная тонкой структуры введена в атомную спектроскопию Арнольдом Зоммерфельдом  в 1916 году [3].  Связана с константами  (e)  и  (h)  соотношением

Учитывая  (7)  и  (9)  получаем связь этой постоянной с  форм-фактором  кольца тока

Рассмотрим условие равновесия движущегося элемента заряда  (q)  по поверхности тора вдоль окружности большого радиуса r_e.  Ток тора-кольца можно рассматривать как совокупность параллельных линейных токов по поверхности тора.  По закону Ампера между ними действует сила притяжения, которая препятствует силе кулоновского отталкивания зарядов одной полярности.  Из модели электрона получено, что  b/r_e  очень мало (≈ 10^-14).  Поэтому можно пренебречь влиянием от зарядов и токов дальних участков тора, а также кривизной кольца.  Решения для линейного заряженного провода с током известны.  В итоге сила, отталкивающая пренебрежимо малый заряд  (q)  от поверхности, равна силе Лоренца, притягивающей этот движущийся заряд  (q)  к центру провода.  Поэтому тор – форма электрона, где решена проблема удержания его заряда.

Вычислим спин электрона – момент импульса вращающей распределенной по кольцу инертной массы электрона по известной формуле  S = mcr_e  с учетом  (11)

что больше известного значения   в 2 раза.

Вычислим магнитный момент кольца по известной формуле  p_m = I_e·πr_e²  с учетом  (7), (3) и (8)

Учитывая  (10)  получаем

что больше известного значения  в 2 раза.

Примечание.  Последние два несоответствия  (S и p_m)  будут разъяснены позднее  в разделе о физическом вакууме, они связаны с механизмом заряда электрона.

Найдем численные значения параметров электрона:

— форм-фактор кольца тока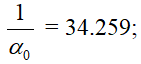 

— радиус электрона-кольца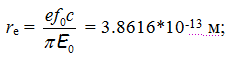

— толщина сечения кольца   = 8.165*10^{-27 м};

— электрическая емкость электрона  C_e = e²/E₀  =  3.1358*10^-25 ф;

(такое же значение электрической емкости имеет сфера классического радиуса  r₀  (1),  если заряд  (e)  распределен на поверхности сферы)

— электрический потенциал на поверхности электрона  U_e = e/C_e =  511 кВ;

— индуктивность кольца электрона  L_e = f₀²/E₀  = 5.2228*10^-17 Гн;

— электрический ток кольца  I_e = f₀/L_e = 39.593 А.

Выводы:

1. Предложена модель электрона в виде тора – заряженного кольца тока смещения комптоновского размера.

2. Найдена интерпретация Эйнштейновской формулы  как суммы двух половинок – кинетической энергии движения по окружности кольца   и энергии кулоновского поля.

3. Размер электрона-кольца соответствует значению комптоновской длины электрона  λ_kompton = 2πr_e.

5. Модель в виде тора решает проблему удержания заряда электрона.

6. Найдена интерпретация постоянной тонкой структуры через форм-фактор кольца тока свободного электрона (коэффициент пропорциональности равен 4).

7. Значения спина и магнитного момента  модели электрона в виде тора отличаются от параметров реального электрона ровно в 2 раза.  Это различие будет исправлено позднее дополнением данной модели механизмом заряда.

Литература

1.  А. Зоммерфельд. Строение атома и спектры. Гос. изд. технико-теоретической литературы, 1956, Том I, Глава I, § 2

(Arnold Sommerfeld. Atombau und Spektrallinien. Braunschweig, Friedr. Vieweg & Sohn. 1951)

2.  Л.Д. Ландау, Е.М. Лившиц.  Электродинамика сплошных сред.  Изд. «Наука», 1982, Том I, Глава I, § 2, стр.22.

3.  М. Борн. Таинственное число 137.  УФН 1936 г,  Том XVI,  вып. 6.

(Max Born.  The mysterious number 137. Lecture delivered to the South Indian Science Association,  Bangalore,  9th of November 1935)

Примечание

 1-ый вариант данного текста был подготовлен 16 апреля 2016 г.

 Текст отправлялся в некоторые физические журналы.  В публикации отказано.

Постоянная тонкой структуры

See english version of this article

Безразмерная  постоянная тонкой структуры  (ПТС)  α  ≈ 1/137  была введена в физику в 1916 году Арнольдом Зоммерфельдом для описания энергетических подуровней, обнаруженных экспериментально в спектрах излучения атомов.  С тех пор было выявлено множество других проявлений этой константы в разнообразных явлениях.  Физики постепенно осознали важность ПТС.  Все основные свойства и характеристики объектов микромира: свойства элементарных частиц, размеры электронных орбит в атомах, энергии связи между атомами и молекулами, и тем самым, все физические и химические свойства вещества определяются величиной этой константы.  В дальнейшем, используя ПТС, удалось разработать весьма результативную теорию – современную квантовую электродинамику (КЭД), с большой точностью описывающую квантовое электромагнитное взаимодействие.

Однако задача теоретического объяснения ПТС не решена до сих пор.  Не удалось найти и математическую процедуру вычисления  ПТС (подобно числу  π).

Знаменитый физик-теоретик середины XX века Ричард Фейнман высказывался о ПТС так:  «С тех пор, как это число открыли свыше пятидесяти лет назад, оно остается тайной.  Все хорошие физики-теоретики выписывают это число на стене и мучаются из-за него. … Хотелось бы знать: выражается это число через  π,  или, может быть, через основание натуральных логарифмов?  Никто не знает.  Это одна из величайших тайн физики: магическое число, которое дано нам, но человек его совсем не понимает … »  (Richard Feynman, “QED: The Strange Theory of Light and Matter”, 1985, p.129).

В 1999 году академик В.Л.Гинзбург писал: «Теоретическая физика еще не может ответить на целый ряд вопросов, например: как построить квантовую теорию гравитации, …, как определить из теории постоянную тонкой структуры …»  (УФН, 1999, №4, с.426).

ПТС  связана с другими физическими константами соотношением 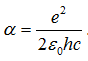 (система СИ).  Официальное значение  постоянной  определяется по некоторой методике комитетом CODATA.

В дальнейшем опираемся на разработанную автором модель электрона.  Запишем указанную выше формулу в виде 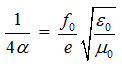 , где магнитный поток электрона  f₀  и его безразмерное представление  можно трактовать как мультипликативный коэффициент для выражений некоторых параметров электрона.  Развивая идеи Майкла Фарадея, Джеймса Максвелла, Генриха Герца  на природу магнитного поля  и на  токи смещения,  разделяя эти токи  на дискретные жилы, автор получил выражение для ПТС  в виде суммы сходящегося математического ряда:

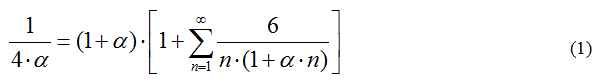
По сути:  левая часть получена на основе аналитической формулы Био-Савара, правая – на основе дискретной модели магнитного поля из вихревых токов смещения.

Примечание:  для упаковки токов смещения автор использовал аналогию – принцип намотки многожильного провода

Найденное выражение (1) не связано с любыми другими физическими константами.  Используя  MatLab,  автором получено значение  равное  137.0156969748.

Официальное значение, равное 137.035999094, является не результатом прямого измерения, а является лишь результатом согласования экспериментальных измерений отношений некоторых физических констант, теоретических моделей и предпочтений  внутри комитета CODATA.

Примечание

1-ый вариант данного текста был подготовлен 11 апреля 2018 г.

Текст отправлялся в некоторые физические журналы.  В публикации отказано.