В XIX веке Максвелл, чтобы получить решение в виде электромагнитной волны, ввел в свои уравнения так называемый ток смещения. В данной работе предлагается модель фотона в виде тора – кольца максвелловского тока смещения.
Пусть r – радиус кольца тора, b – радиус сечения тора (1/2 толщины)
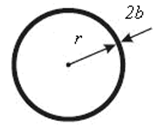
Введем обозначение форм-фактор кольца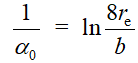
. Тогда формула для индуктивности кольца (ток сосредоточен в поверхностном слое) записываются в виде:
Разобьем энергию фотона на две части
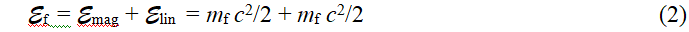
где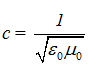 
– скорость света.
Одна часть – это энергия магнитного поля (МП) кольца тока (она же – кинетическая энергия распределенной инерционной массы фотона, вращающейся вдоль кольца)
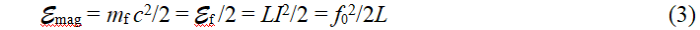
Считаем, что магнитный поток кольца тока фотона (как и электрона) f0 равен известному кванту магнитного потока
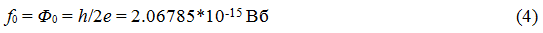
f0 связан с током If и индуктивностью кольца L соотношением
Вторая часть – это кинетическая энергия той же инерционной массы, движущейся линейно в пространстве 
= mf c2/2. Движение инерционной массы фотона происходит в обоих случаях со скоростью света (c), поэтому эти части энергии равны друг другу.
Формула Планка для фотона
поэтому с учетом (1) и (4)
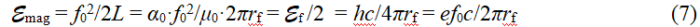
Отсюда получаем формулу для форм-фактора, такую же, как у электрона
Итак, фотон – это кольцо максвелловского тока смещения как у электрона, но без заряда. Такие кольца токов смещения можно увидеть на картинках, нарисованных рукой Генриха Герца в 1889 году при описании своих знаменитых опытов
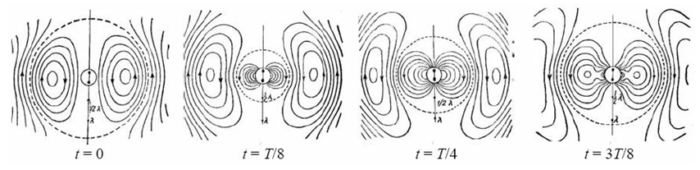
«Силы электрических колебаний, рассматриваемые с точки зрения теории Максвелла»
Рассмотрим цепочку фотонов, образованную передающей антенной (излучательным диполем Герца) или вынужденным испусканием фотонов возбужденными атомами нагретого газа, и находящуюся вдали от источника излучения
Стрелками показано направление вращения тока в цепочке колец, оно чередуется. Соответственно чередуется направление магнитного поля и спина фотонов либо к нам, либо от нас.
Рассмотрим фрагмент плоской монохроматической когерентной ЭМ волны (континуума радио-фотонов) на большом расстоянии от дипольного излучателя, состоящей из множества сфазированных цепочек фотонов
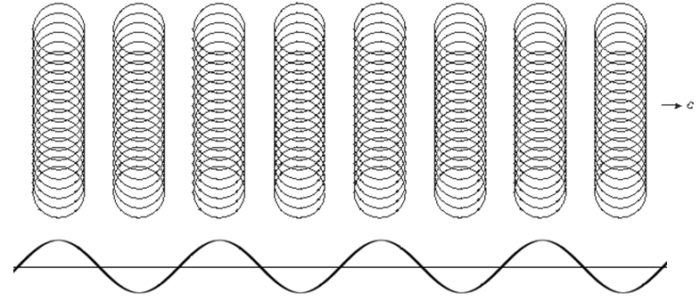
Синусоидальная линия – амплитуда вектора индукции МП, полученная от токов всех колец на основе формулы Био-Савара. Вектор индукции B направлен либо к нам, либо от нас, перпендикулярно рисунку. Такую же форму и фазу имеет напряжение на пробном конденсаторе-антенне, которое интегрируется в этой антенне от токов смещения континуума радио-фотонов при прохождении мимо нее. Диполь антенны и вектор напряженности E электрического поля этого диполя находятся в плоскости рисунка и направлены перпендикулярно направлению движения фотонов.
Результат получается такой же, как на картинках электромагнитной волны современных учебников
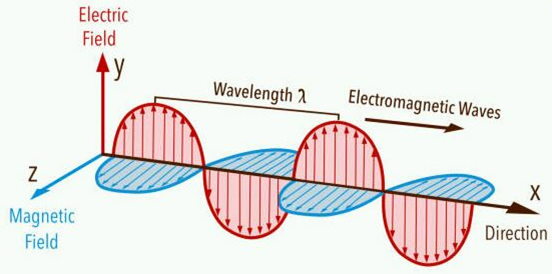
Такой континуум фотонов ведет себя как плоская монохроматическая когерентная волна. Гюйгенс, Френель, Юнг и другие ученые, открывая и исследуя волновые свойства света и используя при этом лучи Солнца, не догадывались что это континуум дискретных фотонов, а не непрерывная волна, наподобие звуковой волны. Тем не менее, на волновом представлении о свете они открыли и разработали законы отражения, преломления, дифракции, интерференции и поляризации света.
Принцип суперпозиции световых волн классической (линейной) оптики, сформулированный Гюйгенсом и Френелем, можно легко заменить принципом суперпозиции фотонов-колец. Существующий более 100 лет парадокс синфазности ЭП и МП получает объяснение новой моделью.
При взаимодействии вещества с потоком фотоном, каждый связанный с ядром электрон можно считать приемной дипольной антенной-конденсатором, преобразующей токи смещения фотонов в электрическое поле. Поэтому модель электромагнитной волны и уравнения Максвелла работают математически верно, хотя физическое единичное взаимодействие фотона со связанным электроном в деталях отличается от такого дипольного представления. Детали взаимодействия фотонов и электронов будут рассмотрены в дальнейшем.
Примечание
1-ый вариант данного текста был подготовлен 16 апреля 2016 г.
