Волна де-Бройля
Мы знаем закон Ампера как взаимодействие двух параллельных токов посредством создаваемых токами магнитных полей (МП).
Однонаправленные токи притягиваются, а противотоки отталкиваются.
Рассмотрим силу взаимодействия двух колец при соосном расположении колец напротив друг друга. Индукция МП от элементарного участка тока кольца на расстоянии R определяется законом Био-Савара и пропорциональна 
. Сила взаимодействия dF между произвольными участками разных колец также пропорциональна , а значит наибольшую долю в общее взаимодействие вносят участки колец, находящиеся на ближайшем между собой расстоянии. В случае токов одного направления (случай притягивания колец) небольшой перекос одного кольца приводит к дальнейшему перекосу равновесия – появлению (увеличению) момента силы, ведущей к дальнейшему повороту кольца в том же направлении (приближающиеся участки колец притягиваются все сильнее, а противоположные расходящиеся – притягиваются все слабее). В случае разнонаправленных колец возникающий момент силы противостоит перекосу.
Итак, случай притяжения магнитных колец-диполей неустойчив к повороту, случай отталкивания – устойчив к повороту. Поэтому при взаимодействии пары свободных колец-диполей, они автоматически разворачиваются в позицию отталкивания между собой. Это утверждение можно обобщить для случая свободного только одного диполя, так и для случаев неодинаковых по размерам диполей. В микромире свободные частицы (магнитные диполи) всегда отталкиваются, за исключением фазы переходного процесса или связанного другими силами статического состояния. Как Землю окружает МП и защищает ее от внешних излучений, также любую частицу окружает МП отталкивания, которое играет роль защитной шубы.
В любой точке дальней зоны, из-за суммирования с разными знаками действия двух полуокружностей кольца-диполя, индукция МП всей частицы-диполя пропорциональна 
. По такому же закону ведет себя сила отталкивания F в целом одного диполя от другого. Энергия взаимодействия МП частиц 
определяется как интеграл от силы взаимодействия и зависит от расстояния как .
Запишем ее в виде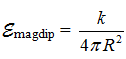 
.
В связи с квадратичной зависимостью величины от расстояния, можно считать мерой плотности потока некоторой абстрактной величины k через поверхность сферы радиуса R из центра сферы. В центре сферы поток абстрактной величины k осуществляется через поверхность сферы радиуса re, а средняя плотность потока k определяется 
– собственной магнитной энергией частицы. Получаем
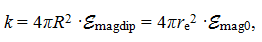
а энергия взаимодействия –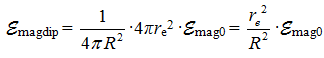 
.
Рассмотрим пример двух сталкивающихся частиц:
Пусть начальная относительная скорость сближающихся частиц равна 
. Тогда кинетическая энергия взаимодействия частиц равна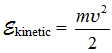 
. Определим Rdb как радиус сферы вокруг частицы 2, достигнув которой извне, частица 1 исчерпает свою кинетическую энергию до нуля и полностью затормозится относительно частицы 2 в результате магнитного отталкивания. Потенциальная энергия магнитного взаимодействия в этот момент равняется начальной кинетической энергии взаимодействия 
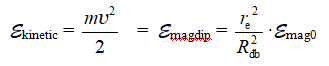
Энергия МП электрона-кольца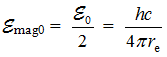 
, масса 
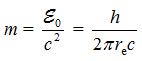(см. текст про Электрон). Учитывая это, получим 
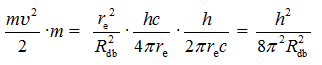или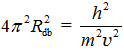 
.
Введя новые величины: длину волны λdb = 2πRdb, импульс 
, и взяв квадратный корень от обеих частей уравнения, получим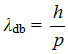 
. Это математическое выражение – суть определение волны де-Бройля частицы.
Вывод
При взаимодействии нейтральных частиц важен не размер керна частицы (шара или кольца), а важен де-Бройлевский размер частицы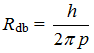 
. Магнитная шуба отталкивания принуждает частицы держаться в фазовом пространстве импульса-расстояния на определенном удалении друг от друга. Можно сказать, что каждой частице в фазовом пространстве необходим объем ∆px·∆x не менее чем h/2π = ћ (если быть точнее то s·ћ, где s – спин). Аналогично для y и z-проекций.
Принцип Гейзенберга ∆p·∆x ≥ ћ
Предложенная в 17 веке Гюйгенсом и развитая в начале 19 века волновая модель света позволила объяснить многие эффекты в оптике: отражение, преломление, дифракцию, интерференцию. В начале 20 века возникло представление о световых квантах. И в 1924 году Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью одних лишь оптических явлений, а присущ также и частицам вещества. Взгляд на любую частицу как на волну позволил сделать прорыв в интерпретации квантовых эффектов, в разработке волновой механики Шредингера. Позднее волновые свойства частиц при взаимодействии с кристаллической решеткой были подтверждены экспериментально.
Творцы квантовой механики отказались от классической детерминированной траектории частицы. Они абстрагировались от лишних вопросов – например, что происходит в деталях с частицей при взаимодействии (или измерении). Они просто постулировали принципиальную невозможность одновременного измерения параметров частицы точнее, чем разрешает соотношение неопределенности ∆p·∆x ≥ ћ. Выше мы показали физические истоки этого ограничения. Посмотрим также на соотношение Гейзенберга для связанных частиц в составе макротел. Ясно, что в кристалле, например алмаза, даже при пренебрежимо малой скорости кристалла, локализация конкретного атома решетки определяется точностью локализации всего кристалла и соотношение неопределенности при этой малой скорости для отдельного атома можно не учитывать. Можно предположить, что это справедливо и в отношении связанного в атоме конкретного электрона. Т.е. точность локализации такого связанного электрона в составе атома определяется точностью локализации ядра и атома в целом и модель фиксированного электрона в атоме не противоречит принципу Гейзенберга.
Ультра-холодные атомы
Современными лазерными методами облако разреженного газа можно загнать в магнитную ловушку и охладить до долей мкК. При такой температуре атомы или молекулы газа выстраиваются в упорядоченную структуру, похожую на кристалл. Магнитная шуба отталкивания заставляет их рассосредоточиться с характерным расстоянием, соответствующим де-Бройлевскому размеру (например, 100 нм). Дополнительные связи притяжения устанавливаются между частицами с помощью джетов (см. далее). Вместе силы отталкивания и притяжения формируют местные потенциальные энергетические ямы, образуя многочастичную квантовую систему.
Интерференция на двух щелях
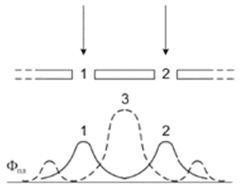
Мы показали, что изменение импульса частицы при взаимодействии с окружением определяется периферийной частью МП, находящейся за де-Бройлевским размером этой частицы. Рассмотрим вопрос – что происходит с МП частицы, когда на пути частицы встречаются две щели. Если частица проходит через 1-ую щель и ее МП не вмещается в размер щели, то периферийная часть его отсекается. При этом какая-то часть периферийного МП (вернее, токов смещения) проходит через 2-ую щель. За щелями эти части, прошедшие через 1-ую и 2-ую щели, начинают взаимодействовать, воссоединяются и определяют дальнейшее направление движения частицы – происходит интерференция 2-х периферийных частей токов смещения. При этом надо учитывать изменения направления и задержки каждой части в процессе движения по разным путям (в волновой модели Гюйгенса-Френеля – изменение фаз). И понятно, что если ширина щелей и расстояние между ними соразмерны де-Бройлевскому размеру частицы, то наблюдаемый эффект интерференции максимален. Интерференция на двух щелях наблюдается как одно частичная, так и много частичная (фотоны или другие частицы должны быть когерентны).
Дифракция фотона за острым краем полуплоскости и огибание препятствий
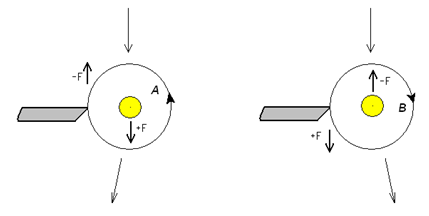
При взаимодействии с острым краем полуплоскости фотон на короткое время цепляется за электроны атомов и затем отрывается с потерей части периферийного МП. Возникающий при этом момент силы подправляет движение фотона либо в сторону тени, либо в светлую область, в зависимости от того, как ориентировано кольцо тока фотона (A и B фотоны). Чем ближе фотон движется к краю полуплоскости, тем больше сила, момент силы и больше отклонение фотона. Далее, отклоненные таким образом фотоны вступают во взаимодействие с электронами атомов экрана. Если два одинаковых фотона одновременно коснулись поверхности экрана в одном месте, то суммирование их МП усиливает взаимодействие с электронами. Если один A-фотон, а другой B-фотон – то взаимодействие с электронами ослабляется или прекращается. Так образуются светлые и темные полосы при интерференции.
Отражение фотона от зеркальной металлической поверхности
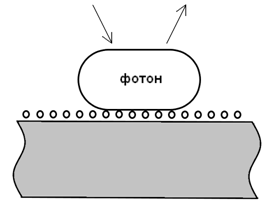
Свободные электроны не вступают в реакцию слияния с фотонами. При соприкосновении одновременно с множеством поверхностных свободных электронов зоны проводимости, кинетическая энергия фотона переходит в энергию упругости фотона-кольца. Кольцо сжимается и затем упруго отражается от поверхности. Поэтому угол отражения равен углу падения.
Магнитное поле протона
Часть МП протона представляет собой вытянутые диаметрально направленные джеты (магнитные струи). Остальная часть МП имеет сферическую форму, аналогично МП нейтрона.
В атомах джеты играют для электронов роль сил отталкивания. Вместе с кулоновскими силами притяжения разноименных зарядов они определяют фиксированное положение электронов в атоме. У каждого протона по два джета, один из которых стандартно замкнут на собственный электрон. Свободные джеты, количество которых зависит от количества протонов и степени ионизации атомов, простираются на большие расстояния. Длину этих джетов можно оценить по существованию в разреженном вакууме Ридберговских атомов размером до 0.1 мм. Джеты являются вращающимися токами смещения и выглядят похожими на тонкие хоботы торнадо (вихри-солитоны вращающегося воздуха).
В 3х-мерном пространстве эти свободные джеты взаимодействуют с джетами других частиц, атомов, молекул, отталкиваясь друг от друга в поперечном направлении, изгибаются и все время зондируют окружающее пространство. Активность джетов зависит от температурных колебаний среды. При встрече с электроном, джеты цепляются за полюса электрона-кольца со свободной стороны, производя обмен импульсами и энергией, отдавая или получая их порции за счет материнского протона. Свободные джеты протонов атомов могут организовывать устойчивые молекулярные связи с другими атомами и молекулами посредством общих электронов.
Можно утверждать, что в атоме вероятность пространственного положения джетов протона (в среднем) описывается волновой функцией уравнения Шредингера. Понятно, почему волновая функция атома антисимметрична, так как антисимметрично дипольное МП фермионов (электронов).
Наличие короны свободных джетов объясняет такие силы и эффекты:
– вандерваальсовские силы магнитного притяжения между молекулами, кинематическая устойчивость которых обеспечивается за счет большой массы молекул и множественности межмолекулярных связей;
– туннельный эффект динамического притяжения временно пойманных электронов (джеты действуют как язык хамелеона при поимке насекомых);
– уравнение Власова для плазмы, учитывающее длинные щупальца джетов;
– эффект Казимира — наличие силы взаимного притяжения/отталкивания незаряженных тел (пластин), находящимися на микронном расстоянии;
– трение – как результат динамического взаимодействия континуума частиц посредством джетов;
– адсорбцию и абсорбцию – притяжение или захват молекул на границе веществ, находящихся в разной фазе (избирательность обуславливается конфигурацией джетов и внешних электронов);
– динамику химических реакций;
– температурную активность биологической микрожизни – взаимные ползание, вращение, ощупывание. Особенно учитывая нежесткость (гибкость) больших органических молекул, похожих на волосатых гусениц (волосы – это джеты);
– самоорганизацию вещества в неживой и живой природе, например кристаллов или живых клеток.
Вид некоторых атомов и их джетов
 | Атом водорода H |
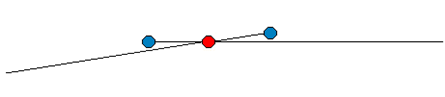 | Атом гелия He (направление МП у этих 2х джетов – противоположное) |
 | Атом неона Ne |
Сверхтекучесть гелия
Свободные джеты атомов гелия могут соединяться с электронами соседних атомов, образуя длинные цепочки атомов – полимолекулы. Энергия такой связи незначительна и стабильность ее возможна только при температуре, близкой к абсолютному нулю.
Полимолекула Гелия-II гладкая, торцы-полюса электронов и собственные джеты ядер молекулы замкнуты друг на друга, полностью терминированы и защищены. У Гелия-II нет акцепторов, которыми он может тормозиться при своем движении или соединяться в поперечные связи для образования конденсированного состояния. Поэтому Гелий не замерзает даже при абсолютном нуле, так как весь соединяется в полимолекулы. Полимолекулы Гелия-II имеют большую длину и гибкость, что позволяет им передвигаться по трещинам на макро расстояния, даже вертикально по стенкам.
Сверхпроводимость
При протекании тока в сверхпроводнике электроны зоны проводимости образуют длинные и замкнутые цепочки, взаимно защищая свои торцы-полюса, не позволяя внешним джетам цепляться за них. Устойчивость режима магнитного притяжения между отрицательными электронами-кольцами обеспечивается общим многократно усиленным магнитным полем сформированного длинного замкнутого соленоида.
Похожая конфигурация МП у установок удержания плазмы Токамак.
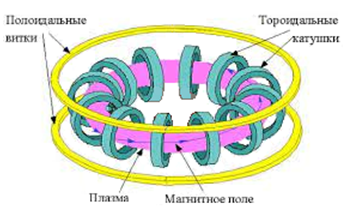
В нашем случае роль тороидальных витков выполняет вращение электронов (ток колец), роль полоидальных – групповое поступательное движение электронов.
Дополнительную роль в сохранении цепочек играет механическая динамика – инерция вращения и поступательного движения электронов.
Условие образования цепочки – удачная конфигурация решетки, наличие канала с минимальным количеством свободных (опасных) джетов в его окрестности. При низкой температуре активность джетов решетки уменьшается – они становятся малоподвижными, и цепочки электронов находят пустые лазейки в решетке атомов. Скорость электронов-носителей должна превышать тепловую скорость окружающих электронов.
Взаимодействие оптических фотонов с электронами атомов
Энергия оптического фотона должна быть меньше, чем энергия связи электрона с ядром атома. Со свободным электроном слияние фотона с электроном не произойдет, электрон не может увеличить свою внутреннюю энергию (она фиксирована внутренним устройством кольца-заряда электрона). Плоскость кольца фотона (и направление его движения) должна примерно совпадать с плоскостью кольца электрона и быть перпендикулярной джету, на котором сидит электрон. При соприкосновении оптического фотона с таким электроном, кинетическая энергия фотона переходит в упругую поперечную энергию джета, фотон начинает останавливаться с одновременной попыткой слияния тока кольца фотона с током кольца электрона. Если параметры фотона удовлетворяют допустимому более высокому устойчивому энергетическому состоянию – фотон поглощается электроном. Если нет – то джет протона, с висящими на нем частично сливающимися кольцами электрона и фотона, описав круг 360°, выбрасывает фотон как из пращи, сохранив его прежние направление и энергию. Такая процедура задерживает фотон на некоторое время. Длительность и количество попыток слияния фотонов с электронами атомов определяют реальную скорость распространения света в конкретном веществе, его оптическую плотность.
Этот механизм объясняет эффект увлечения света потоком жидкости в опытах Физо в 1851 году.
Этот механизм объясняет правило отбора при переходах между атомными состояниями ∆l = ±1, т.к. кинетическая энергия фотона сохраняется в поперечном изгибе джета атома, а изгиб джета соответствует орбитальному квантовому числу l.
Трение между поверхностями
Можно утверждать что трение – это результат динамического взаимодействия континуума поверхностных частиц посредством джетов. Взаимодействие происходит как при непосредственном касании поверхностей, так и при разделении поверхностей слоем вакуума. Интересно, что возможны условия, при которых заполнение вакуумного промежутка разреженным газом не увеличивает силу трения, а уменьшает. Это происходит из-за того, что молекулы газа играют роль шариков-катков между джетами поверхностей.
Подтверждением вышесказанного можно привести экспериментальные исследования, проведенные в 2007-2012 годах профессором Самохваловым В.Н. (доступно в Интернете).
Исследования динамических взаимодействий двух близкорасположенных дисков в условии вакуума производились последовательно на разном оборудовании в нескольких организациях:
— Научно-исследовательский центр космической энергетики Самарского государственного аэрокосмического университета;
— лаборатория Самарского государственного университета путей сообщения;
— установка глубокого вакуума Института катализа СО РАН (г. Новосибирск).
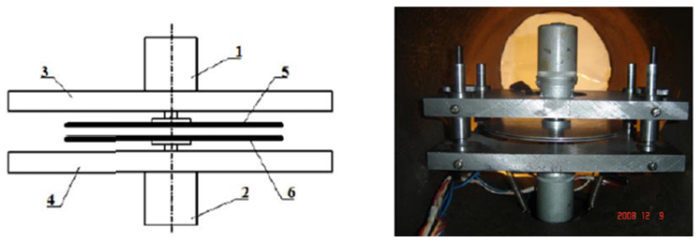
Схема и фотография устройства для исследования динамических эффектов в вакуумной камере:
1 и 2 – электродвигатели постоянного тока; 3 и 4 – диски из разных материалов, диаметром 165 мм и толщиной от 0,9 мм. Зазор между дисками варьировался в диапазоне 1,5 – 4,0 мм.
Основным экспериментальным результатом исследований является то, что в диапазоне остаточного давления воздуха от 0,1 до 0,001 Торр величина силового воздействия вращающего диска на пассивный неподвижный диск увеличивается в несколько раз с ростом глубины вакуума. Это относится и к силе отталкивания дисков друг от друга (в направлении нормали к поверхности), и к тангенциальному увлечению одного диска другим.
