Предложена модель атома с фиксированным расположением электронов, имеющих комптоновский размер. Модель опробована для расчета энергетических термов и размера простых атомов и молекул. Фиксированная конструкция модели позволяет делать расчет атомов практически алгебраическим методом, не прибегая к вычислению волновых функций или функционалов плотности. Модель применима для сложных атомов и молекул, и может найти применение в химии и в наноиндустрии.
Сокращения: ЭП – электрическое (кулоновское) поле, МП – магнитное поле
1. Электрон
В 1897 году Джозеф Томсон открыл электрон. Был определен заряд электрона (e), ставший квантом электрического заряда. Предложена форма электрона в виде шара и определен радиус шара исходя из законов электростатики. Сделана попытка отождествления массы-энергии электрона через энергию электрического поля этого шара. Получилось некоторое расхождение в массе электрона.
В 1923 году Артур Комптон провел эксперименты по рассеиванию рентгеновских лучей на свободном электроне. При математическом описании этого эффекта выявлен линейный размер 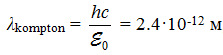 , который назвали Комптоновской длиной волны электрона. Тогда же были попытки представить электрон в виде кольца соответствующего размера. Но в 1925 году рождался эффективный инструмент микромира – квантовая механика, и для нее больше подходил электрон в виде материальной точки, локализация которой в пространстве описывается вероятностной функцией.
, который назвали Комптоновской длиной волны электрона. Тогда же были попытки представить электрон в виде кольца соответствующего размера. Но в 1925 году рождался эффективный инструмент микромира – квантовая механика, и для нее больше подходил электрон в виде материальной точки, локализация которой в пространстве описывается вероятностной функцией.
Но вопросы остались
1. Как устроены электрон и атом?
2. Почему в электромагнитной волне электрическое и магнитное поля представлены равноправно, а в атомной модели Нильса Бора и в уравнении Шредингера роль МП второстепенна?
3. Что делать с проблемой излучения движущегося заряда (электрона)?
4. Каковы механизмы устойчивости множества электронов (атомных орбиталей) и обеспечения жесткости атомов, молекул, кристаллов ? Ведь, известна задача нестабильности трех тел в поле 1/R2, известна теорема Ирншоу, доказывающая, что чисто электростатические системы не могут быть устойчивыми.
Формула Планка-Комптона 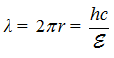 одинакова для электрона и фотона. Она происходит из формулы тока кольца
одинакова для электрона и фотона. Она происходит из формулы тока кольца ![]() (чем короче путь тока – тем больше значение тока и энергия его МП). Электрон и фотон – частицы-родственницы. Собственная энергия электрона состоит из двух частей – энергии МП кольца и энергии ЭП (для свободного электрона обе части равны).
(чем короче путь тока – тем больше значение тока и энергия его МП). Электрон и фотон – частицы-родственницы. Собственная энергия электрона состоит из двух частей – энергии МП кольца и энергии ЭП (для свободного электрона обе части равны).
Энергия фотона состоит из двух равных частей – кинетической энергии вращения фотона (энергия МП кольца) и кинетической энергии линейного движения фотона в целом со скоростью света (![]() — инерционная масса фотона)
— инерционная масса фотона)
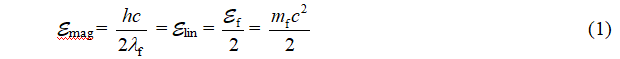
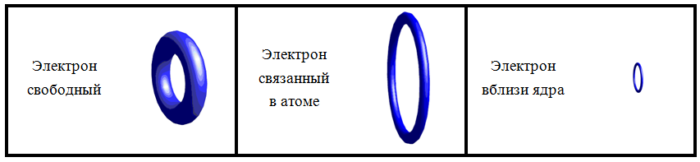
Кольцо электрона способно расслаиваться на два кольца – собственно электрон (с меньшей энергией, чем у свободного электрона) и фотон. И способно вновь воссоединяться. Кольцо фотона электрически нейтральное. Кольцо электрона дополнительно несет заряд (e). В сопутствующей системе координат у фотона отсутствует кинетическая энергия линейного движения и в формировании размера фотона принимает участие только энергия его МП. В формировании размера электрона принимает участие энергия и МП и ЭП, поэтому по сравнению с фотоном он имеет меньшие в 2 раза размер и спин (см. ранее), и большее в 2 раза гиромагнитное отношение.
Соотношение Планка-Комптона 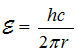 широко использовалось в 20 веке для оценки параметров открытых экспериментально новых частиц. Предполагаем, что это соотношение применимо ко всему микромиру, и что микромир состоит из вихревых элементов (кольцевых токов). Про эти вихревые частицы-атомы предположил Рене Декарт еще 4 века назад.
широко использовалось в 20 веке для оценки параметров открытых экспериментально новых частиц. Предполагаем, что это соотношение применимо ко всему микромиру, и что микромир состоит из вихревых элементов (кольцевых токов). Про эти вихревые частицы-атомы предположил Рене Декарт еще 4 века назад.
2. Модель строения атома (формально-математический подход)
Будем искать энергетическое уравнение равновесия электрона в поле ядра при условии фиксированного положения электрона, т.е. равенства нулю его кинетической энергии.
Собственная внутренняя энергия электрона состоит из двух частей ![]() . Заряд свободного или связанного электрона один и тот же – (e). Поэтому энергия его заряда
. Заряд свободного или связанного электрона один и тот же – (e). Поэтому энергия его заряда 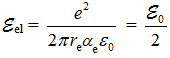 является константой. Это эквивалентно условию
является константой. Это эквивалентно условию

где индекс 0 соответствует свободному электрону, а индекс e – связанному в атоме электрону.
Энергия МП электрона свободного 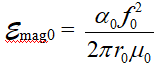 и связанного
и связанного 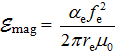 разная.
разная.
Поэтому разница ![]() собственных энергий свободного и связанного в атоме электрона будет равна разнице энергий их МП
собственных энергий свободного и связанного в атоме электрона будет равна разнице энергий их МП
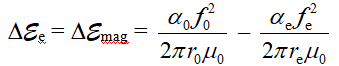
С другой стороны энергия кулоновской связи электрона с ядром атома (потенциальная энергия электрона в поле ядра, без учета знака) равна
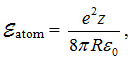
где z – кратность заряда ядра, а R – радиус атома (расстояние между электроном и ядром). Приравняем эту энергию связи ![]() разнице собственных энергий свободного и связанного электрона
разнице собственных энергий свободного и связанного электрона ![]() (насколько свободный электрон потерял энергию, излучив фотон, – настолько он стал привязан к ядру атома)
(насколько свободный электрон потерял энергию, излучив фотон, – настолько он стал привязан к ядру атома)
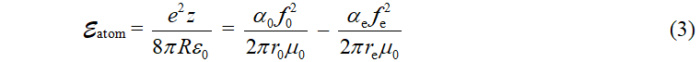
Учитывая, что для свободного электрона энергия МП равна энергии его ЭП
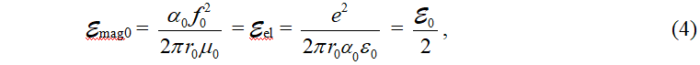
левую часть (кулоновскую энергию связи) уравнения (3) можно привести к следующему виду
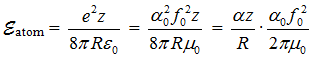 , где
, где 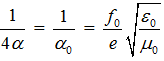 (см. текст Электрон).
(см. текст Электрон).
Обозначив 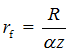 – радиус условного фотона-кольца, уравнение (3) приведем к виду
– радиус условного фотона-кольца, уравнение (3) приведем к виду

Или с учетом (2)
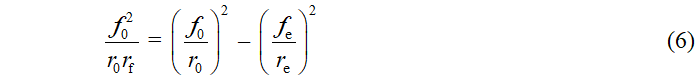
Разность квадратов правой части должна быть квадратом. Поэтому ![]() равное
равное ![]() должно быть тоже квадратом, а именно
должно быть тоже квадратом, а именно ![]() , при условии
, при условии 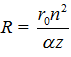 , где n = 1, 2, 3, … ∞. Экспериментально это подтверждено 100 лет назад. В итоге разрешенные уровни энергии (термы) связанного электрона равны
, где n = 1, 2, 3, … ∞. Экспериментально это подтверждено 100 лет назад. В итоге разрешенные уровни энергии (термы) связанного электрона равны
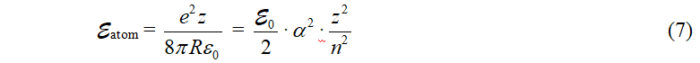
Расстояние от ядра до электрона равно 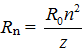 , где
, где ![]() – боровский радиус атома водорода. Мы получили выражение энергетических термов водородоподобного атома с помощью модели, отличной от моделей Нильса Бора или Шрёдингера.
– боровский радиус атома водорода. Мы получили выражение энергетических термов водородоподобного атома с помощью модели, отличной от моделей Нильса Бора или Шрёдингера.
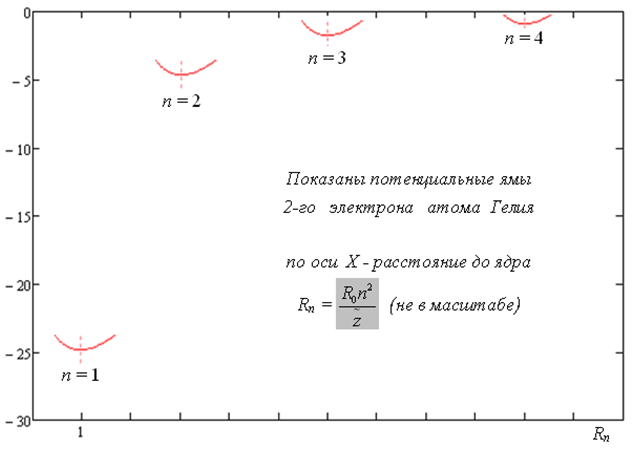
Условие квадратичности правой части уравнения (6) формирует локальную потенциальную яму в точке, в которой это уравнение выполняется. Физический механизм возникновения локальной потенциальной ямы для каждого электрона – трансформация формы и изменение параметров электрона в суммарном кулоновском поле окружения (ядра и других электронов). Это является причиной квантования энергии электрона в атоме, формирования уникального спектра атома и вообще причиной существования квантового микромира.
3. Физическое обоснование предложенной модели атома
Энергетическое уравнение (3) запишем в следующем виде (умножив левую и правую часть на ![]() )
)
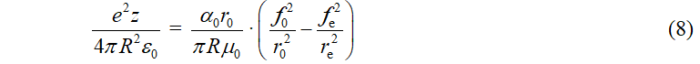
Мы видим, что выражение в левой части — это сила кулоновского притяжения между электроном и ядром 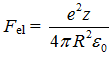 , правая часть отвечает за МП и очевидно, что сила
, правая часть отвечает за МП и очевидно, что сила 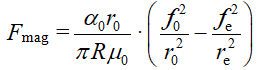 – это сила отталкивания между магнитными диполями электрона и ядра. Т.е. сила электрического притяжения между ядром и электроном уравновешивается силой магнитного отталкивания. И зависимость силы МП от расстояния R до ядра ведет себя как
– это сила отталкивания между магнитными диполями электрона и ядра. Т.е. сила электрического притяжения между ядром и электроном уравновешивается силой магнитного отталкивания. И зависимость силы МП от расстояния R до ядра ведет себя как ![]() , т.е подобно центробежной силе модели Нильса Бора (поэтому модель Бора подошла в 1913 году). Но как же так, скажете вы, согласно закона Био-Савара индукция (и сила) МП кольца тока (магнитного диполя) должна убывать с расстоянием как
, т.е подобно центробежной силе модели Нильса Бора (поэтому модель Бора подошла в 1913 году). Но как же так, скажете вы, согласно закона Био-Савара индукция (и сила) МП кольца тока (магнитного диполя) должна убывать с расстоянием как ![]() при R>>re. Можно предположить, что в микромире концентрация энергии в протоне изменяет геометрию МП протона. Из-за кругового тока (вращения) МП вытягивается вдоль оси кольца и сужается в радиальном направлении (аналогия – хобот торнадо).
при R>>re. Можно предположить, что в микромире концентрация энергии в протоне изменяет геометрию МП протона. Из-за кругового тока (вращения) МП вытягивается вдоль оси кольца и сужается в радиальном направлении (аналогия – хобот торнадо).
Здесь уместно сослаться на мнения таких авторитетов как Уильям Клиффорд (1870), Альберт Эйнштейн (1916) и Джон Уиллер (1965), которые высказывали предположение об изменении кривизны пространства около сгустков энергии-массы в рамках геометрического подхода к описанию физического мира. Из-за этого же эффекта меняется и размер электрона вблизи протона, нейтрона и всего ядра («эффект сжатия» наблюдается в нуклонах, в ядрах атомов, в атомах и даже в звездах). В непосредственной близости от одиночного нуклона размер электрона уменьшается в 2000 раз, а внутри структуры сложных ядер еще на 1-2 порядка. Поэтому эксперименты по рассеиванию электронов на ядрах дают размер электрона порядка 10-16 — 10-18 м. Трансформация электрона и других частиц в центрах концентрации энергии-массы открывает путь к построению реалистичных моделей составных частиц — нуклонов и ядер.
Рассмотрим, как исторически в физике видоизменялась модель взаимодействия между ядром и электроном. Вначале была орбитальная модель Нильса Бора, где роль отталкивающей силы была возложена на центробежную силу, хотя модель и противоречила представлению об излучении заряда, двигающего с ускорением. Затем появилась модель Шредингера с абстрактными орбиталями, где вообще ушли от физического движения электрона в атоме, игнорируя проблему излучения и заменив координаты электрона на плотность вероятности его нахождения в пространстве атома как функцию от координат. В последующем, в квантовой электродинамике перешли к еще более абстрактной модели, заменив физическое взаимодействие атома и электрона на обменное взаимодействие посредством обменных частиц — виртуальных фотонов. При этом неявно уравняли пространственную эффективность электрического и магнитного полей в атоме, т.к. у электромагнитной волны (фотона) ЭП и МП энергетически равноправны.
4. Соотнесение атомных состояний к геометрии модели атома
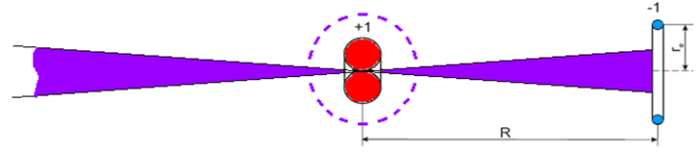
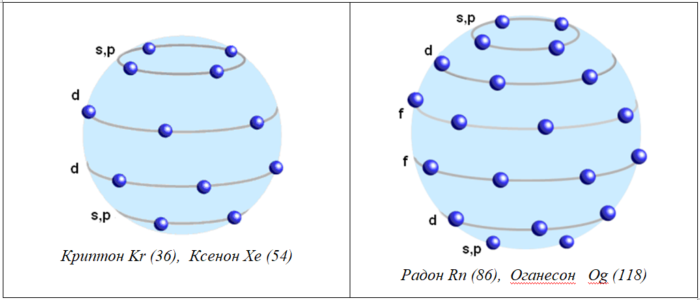
Электроны s — типа располагаются на прямолинейных джетах, где кулоновская сила притяжения электрона к ядру уравновешивается упругой силой продольного сжатия магнитного джета материнского протона.

Электроны p, d и f — типа располагаются на изогнутых джетах, где кулоновская сила притяжения электрона к ядру уравновешивается векторной суммой упругих сил продольного сжатия и поперечного изгиба магнитного джета материнского протона.
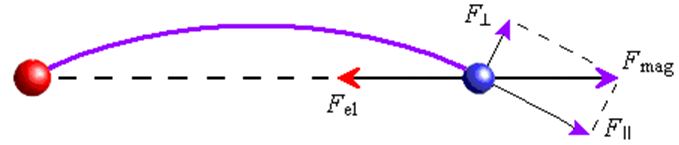
Излучение электроном фотона происходит посредством расслоения кольца электрона на два: собственно электрона с меньшей энергией МП и фотона-кольца. Разница энергии упругого продольного сжатия джета переходит в энергию МП фотона, а разница энергии поперечного изгиба – в кинетическую энергию линейного движения фотона со скоростью света. Т.е. поперечный изгиб джета является накопителем кинетической энергии фотонов при излучении и поглощении фотонов. Так как изгиб джета соответствует орбитальному квантовому числу l, этот механизм объясняет известное правило отбора ∆l = ±1 при переходах между атомными состояниями.
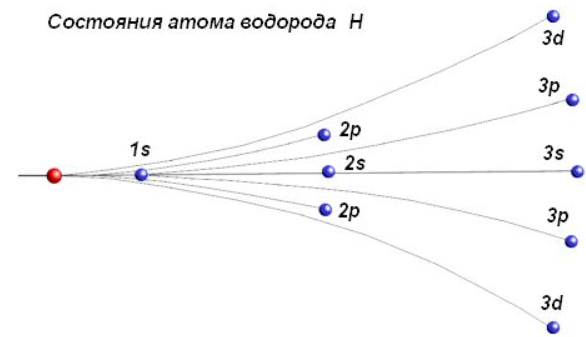
Главное квантовое число n определяет радиус сферы на которой располагаются электроны.
Орбитальное квантовое число l определяет степень изгиба джета и радиус окружности (на поверхности сферы), на которой располагаются электроны.
Магнитное квантовое число m определяет направление изгиба джета – полярный угол расположения электронов на окружности l.
Квантовое число s (спин) различает два электрона, находящиеся диаметрально противоположно в разных полушариях.
Пример сложного атома:
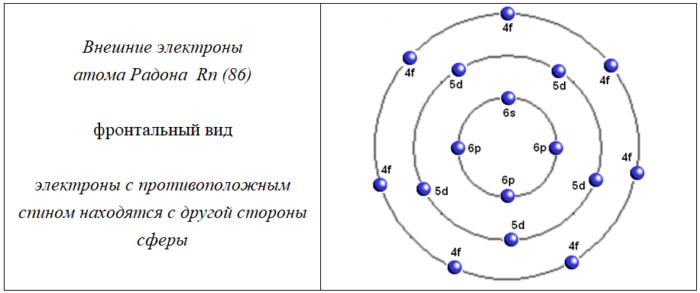
5. Обобщение уравнения энергетических термов для сложных атомов и молекул
Формула (7) верна не только для водородоподобного атома, но и для любых других атомов и сложных молекул, надо только рассчитать эффективные ![]() для каждого электрона и геометрически согласовать с другими электронами. Отметим что положение электрона в нашей модели – фиксированное в пространстве. Это облегчает задачу нахождения энергии термов и значительно проще, чем вычисление плотностей орбиталей.
для каждого электрона и геометрически согласовать с другими электронами. Отметим что положение электрона в нашей модели – фиксированное в пространстве. Это облегчает задачу нахождения энергии термов и значительно проще, чем вычисление плотностей орбиталей.
Уравнение (3) для водородоподобного атома можно обобщить на случай наличия окружения из других зарядов. Для этого силу, действующую на электрон (обозначен индексом 1) запишем в виде F1 = e·E1. Напряженность ЭП в точке нахождения электрона определяется векторным сложением 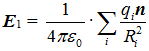 , где qn – все заряды окружения (электронов и ядер атомов, в т.ч. и нашего ядра с индексом 1),
, где qn – все заряды окружения (электронов и ядер атомов, в т.ч. и нашего ядра с индексом 1), ![]() – их расстояния до нашего электрона, n – единичный вектор направления. Действие всех зарядов можно привести к действию условного заряда, присвоенному нашему ядру
– их расстояния до нашего электрона, n – единичный вектор направления. Действие всех зарядов можно привести к действию условного заряда, присвоенному нашему ядру 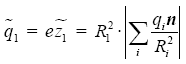 или для параметра – кратности заряда
или для параметра – кратности заряда 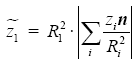 .
.
В итоге энергетическое уравнение (3) для выбранного электрона (обозначен индексом 1) сложного атома или молекулы запишется в виде
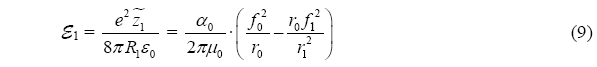
В молекулах данная модель подходит для вычисления энергии ионных, ковалентных, водородных видов связей (и даже вандерваальсовских с некоторой коррекцией). Для нахождения термов и геометрии структур необходимо применять метод итераций. Задача упрощается для симметричных структур. Расстояние от ядра до электрона находится легко 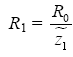 , где
, где 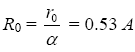 . Также с помощью вычислительных методов можно определить градиент силы, действующей на электрон на дне локальной потенциальной ямы и определить коэффициент жесткости силы для расчета колебательных спектров или параметров макро-комплексов, например кристаллов. По глубине ям можно вычислить интенсивности спектральных линий излучения.
. Также с помощью вычислительных методов можно определить градиент силы, действующей на электрон на дне локальной потенциальной ямы и определить коэффициент жесткости силы для расчета колебательных спектров или параметров макро-комплексов, например кристаллов. По глубине ям можно вычислить интенсивности спектральных линий излучения.
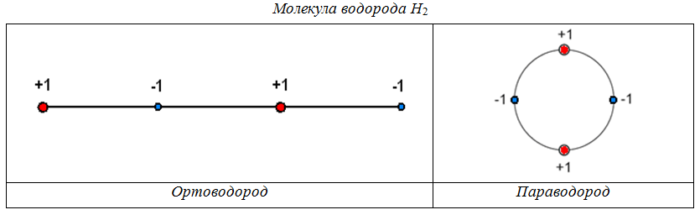
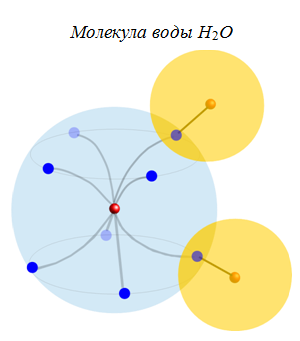
6. Примеры 3D-моделей некоторых атомов и молекул
(показаны внешние оболочки)

7. Расчет простых атомов с указанием точности результата
Форма результата: результат (эксперимент, ~точность). Обозначение: β = π/137 = ~0.023.
Ион водорода H־
(![]() = 13.59+0.76 = 14.35 ev, 0.76 и 13.59 – энергии отрыва 2 и 1 электронов)
= 13.59+0.76 = 14.35 ev, 0.76 и 13.59 – энергии отрыва 2 и 1 электронов)


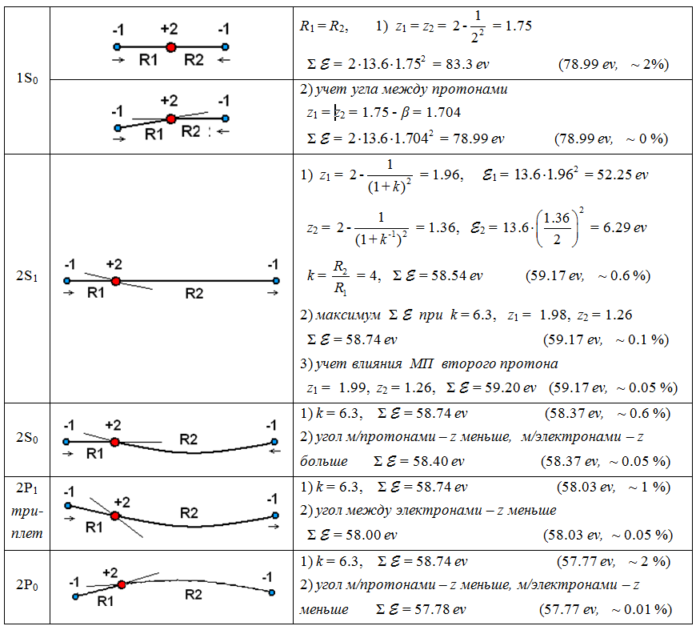
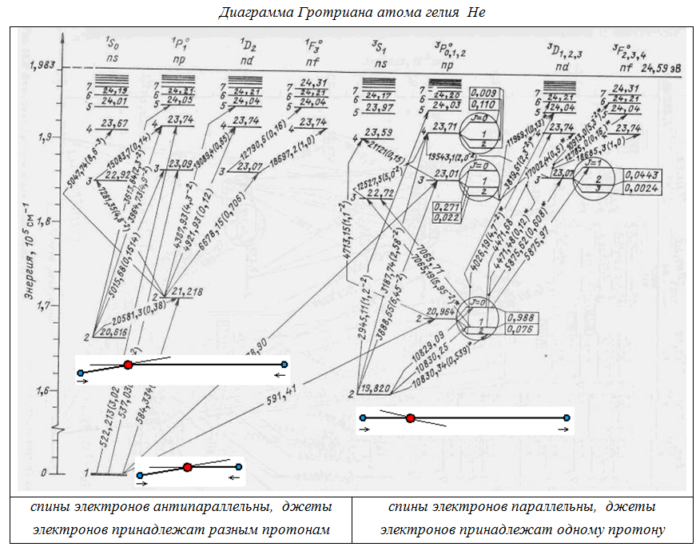
Пример формулы для расчета конкретного значения суммарной энергии связи атома гелия для двух электронов. Формула найдена на основе уравнений (7), (9) и геометрических построений.
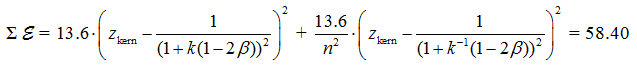
где n = 2 — уровень орбиты 2-го электрона (главное квантовое число); ![]() – кратность заряда ядра;
– кратность заряда ядра; 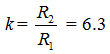 – отношение расстояний от ядра до электронов, значение 6.3 — при максимуме
– отношение расстояний от ядра до электронов, значение 6.3 — при максимуме ![]() ;
; 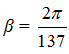 – малый параметр (угол), который применяется для учета угловых добавок. Коэффициент при β – целое число, в данном примере равное 2, зависит от орбитального квантового числа l и конфигурации протонов ядра. Подобный подход позволяет получить точность вычисления термов около 0.05 %, в т.ч. и для других атомов, не только гелия.
– малый параметр (угол), который применяется для учета угловых добавок. Коэффициент при β – целое число, в данном примере равное 2, зависит от орбитального квантового числа l и конфигурации протонов ядра. Подобный подход позволяет получить точность вычисления термов около 0.05 %, в т.ч. и для других атомов, не только гелия.
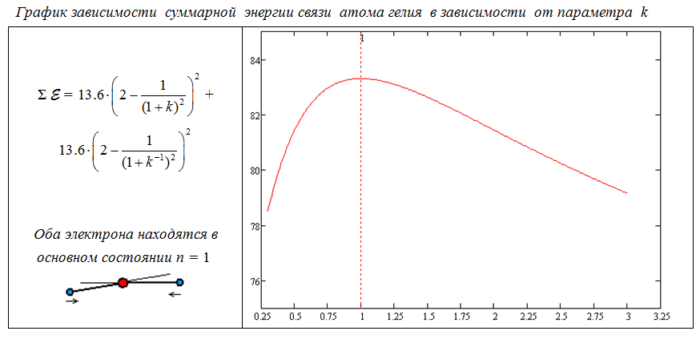
Можно сказать, что взаимодействие ЭП и МП ядра и электронов создают в атоме сетку потенциальных ям, в центре каждой из которых для электрона существует местный локальный минимум энергии.

8. Графический симулятор атомов и молекул на основе физической модели статического атома
Проект коммерческих программных продуктов для персонального компьютера
| № | Наименование этапа и продукта |
| 1 | 3D редактор-конструктор атомов и молекул для учебных целей |
| 2 | 3D редактор-конструктор атомов и молекул для стереохимии с аналитическим расчетом химических параметров (пространственные координаты всех электронов, энергия связи каждого электрона с остовом, электрическая поляризуемость по выбранному направлению) |
| 3 | 3D редактор-конструктор атомов, молекул, кристаллов, ассоциатов, больших молекул, наноматериалов, гетероструктур и бионанороботов для химиков, технологов, материаловедов, вирусологов |
| 4 | 3D редактор-конструктор атомов и молекул спектральной точности для физических исследований (расчет атомных, колебательных и вращательных термов, расчет интенсивностей термов, сопряжение с эмпирическими базами спектров) |
Примечание
Доклад – “Статическая модель атомов и молекул” – доложен автором на меж институтском семинаре ИАиЭ СО РАН 09.10.2018 г.